介绍

点扩散函数（PSF）是点状物体在显微镜下的三维图像。它描述了显微镜如何由于光的衍射而模糊任何点状物体，这决定了显微镜的分辨率极限。PSF 可用于评估显微镜的轴向分辨率和横向分辨率。轴向分辨率是沿光轴的两点相互接近且仍能分辨的最小距离，而横向分辨率是同一焦平面上的两点相互接近且仍能分辨的最小距离。PSF 受多种因素影响，例如物镜的数值孔径和聚光器、所用光的波长、介质的折射率以及光学元件的对准和质量。更高的数值孔径、更短的波长、更高的折射率以及更好的对准和质量可以提高 PSF，从而提高显微镜的分辨率。

显微镜分辨率是显微镜区分标本或样品细节的能力。它也可以定义为样本上仍可区分为独立实体的两点之间的最小距离。该值越小，显微镜的分辨力越高，图像的清晰度和细节越好。光学显微镜的理论分辨率极限约为 200 nm，这比许多分子和原子的尺寸要大得多。这个物理极限被称为阿贝极限，以 Ernst Abbe 的名字命名，他于 1873 年首先提出了这个概念。

限制光学显微镜分辨率的一个因素是衍射，这是光线在穿过小开口或绕过障碍物时发生的弯曲。衍射产生我们所说的 PSF。衍射导致光散开并形成干涉图案，从而模糊标本的图像。当孔径（控制进入镜头的光量的开口）较小时，衍射会更加明显。圆形孔径的衍射图案有一个中央亮点，周围环绕着同心光环，称为艾里斑。艾里斑的大小取决于光的波长和透镜的数值孔径（透镜可以收集多少光的量度）。

仔细观察 PSF 

当使用显微镜形成微小点光源的图像时。点扩散函数定义了点源图像的外观。要获得点扩散函数的最准确视图，您需要查看低于显微镜理论分辨率极限的单点光源。让我们想象一下，我们正在对一个荧光珠进行成像，该球体融合了荧光团并且低于显微镜的分辨率极限，当我们想要凭经验测量显微镜的 PSF 时，我们实际上使用荧光珠。当我们查看珠子的横向光学图像时，我们会看到一个比珠子本身大的斑点，并且它有一个模糊的边缘。如果我们增强图像对比度，我们可以看到较弱的强度值，明亮的中心被深色和浅色的同心环包围。如果我们在该图像上画一条线，并通过该线查看图像的强度，我们将看到我们称为最大值的明亮中心具有类似高斯的分布，而外环比最大值暗得多。 

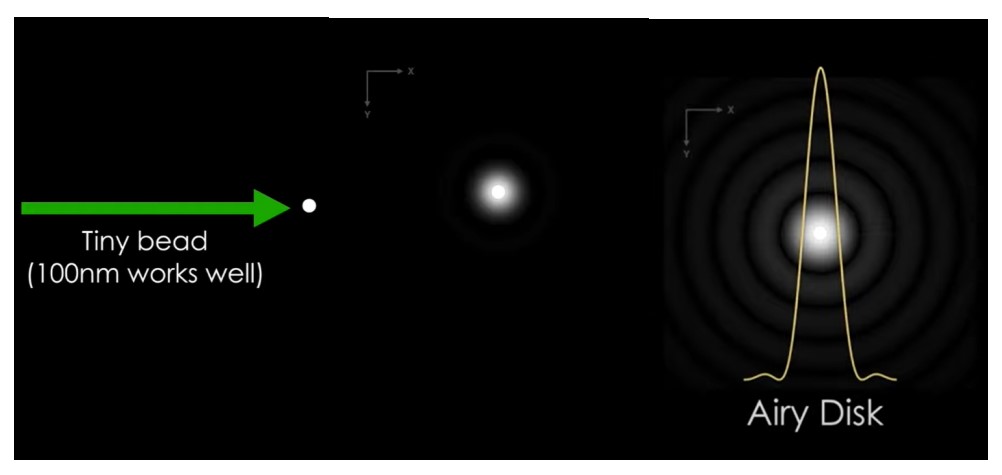
PSF 源于衍射和干涉

衍射是波通过狭窄孔径或绕过障碍物时的弯曲。这是因为波在穿过孔径或障碍物后会扩散并相互干扰。衍射是所有类型的波（例如激光波、声波、水波和物质波）都会出现的波特征。干扰是两个或多个波相加而产生新的波型。它发生在波浪重叠并建设性或破坏性地结合时关于他们的相位差。干扰也是一种波的特征，所有类型的波都会出现。衍射和干涉之间的区别在于，衍射涉及由于孔径或障碍物导致的单个波的弯曲，而干涉涉及由于叠加而导致的两个或多个波的组合。衍射和干涉经常同时发生，例如在衍射光栅或双缝实验中。

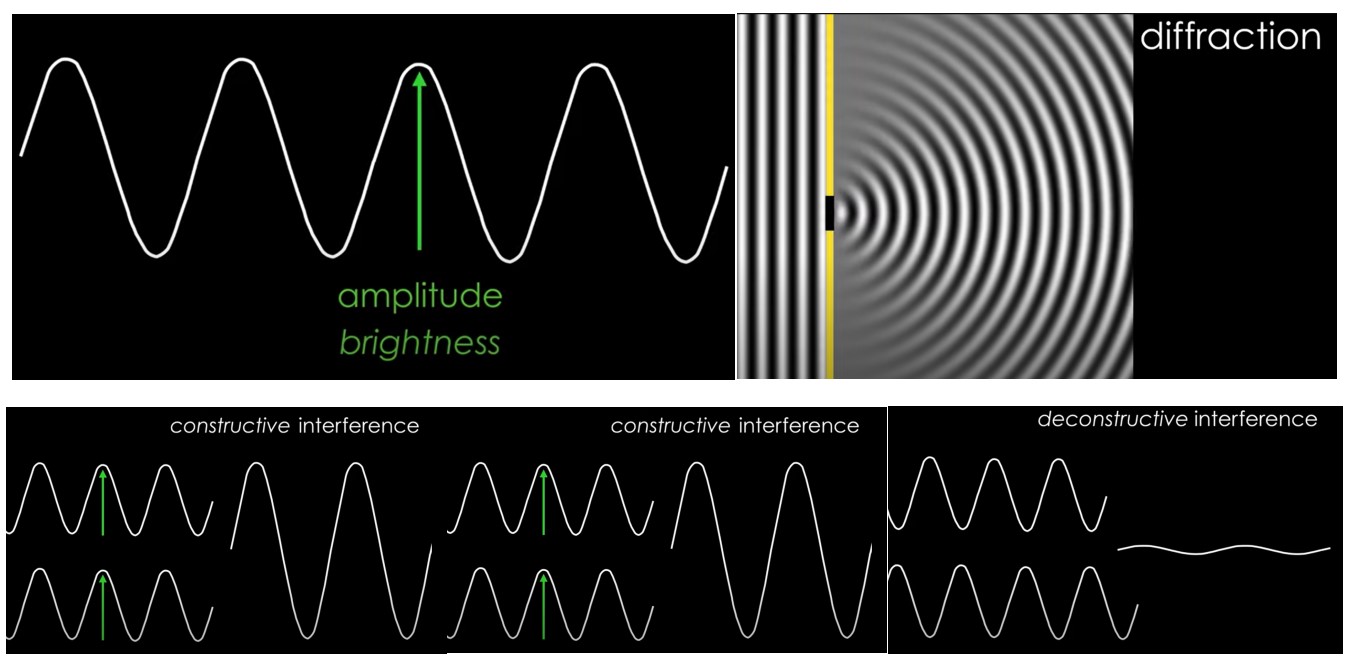
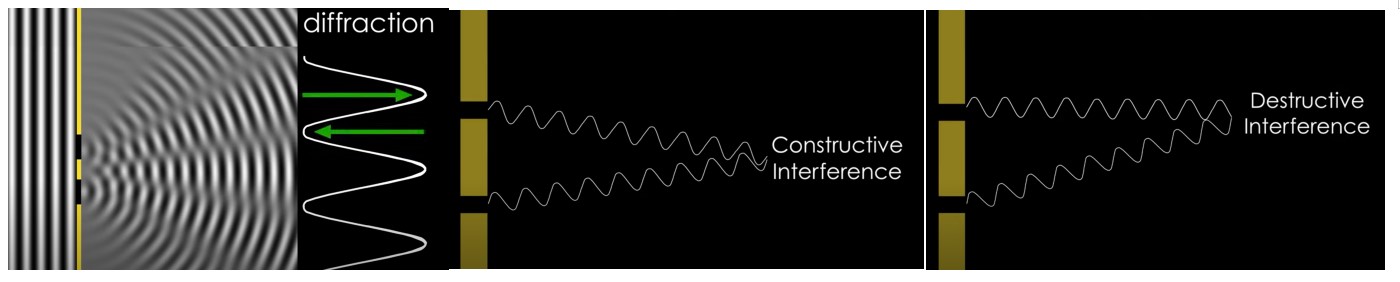
显微镜中的衍射

显微镜中的衍射是一种现象，当光波通过障碍物（例如孔径或标本）并在其周围弯曲时发生。衍射使光波散开并相互干涉，形成衍射图案。衍射限制了显微镜的分辨率，因为它阻止了点源或物体的图像变得无限清晰。相反，点源或物体的图像被模糊到称为 PSF 的有限区域中。衍射的程度取决于光的波长和物镜的数值孔径 (NA)。更短的波长和更高的 NA 值导致更少的衍射和更好的呃决议。显微镜的分辨率极限大约是光波长除以 NA 的一半。这个极限也被称为衍射势垒。为了克服这个障碍，一些超分辨率显微镜技术使用特殊方法来操纵衍射图案或定位超出衍射极限的单个分子。

PSF 对图像的影响 

PSF 对图像的影响是它降低了标本细节的清晰度和对比度。PSF 使点光源或物体的图像模糊成一个有限区域，该区域大于光源或物体的实际尺寸。这意味着如果两点源或对象比 PSF 的大小更近，则它们无法作为图像中的单独实体进行解析。PSF 还会影响图像的强度或亮度，因为它会将来自点光源或物体的光散布到大面积上。PSF 还会在图像中的锐边或明亮特征周围引入伪影，例如振铃或光晕效果。

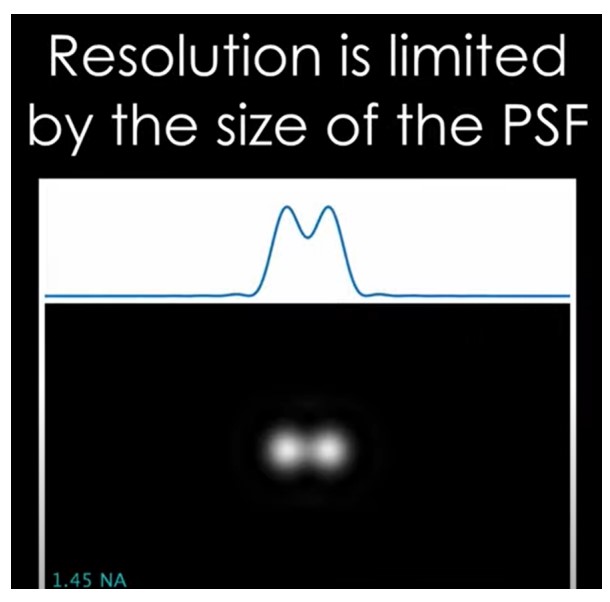
分辨率方程

根据所涉及的假设和因素，计算显微镜分辨率有不同的公式。最常见的公式之一是 Ernst Abbe 公式，由下式给出：

• 分辨率 (r) = 0.61λ/NA

其中 r 是分辨率，λ 是来自物体的光的波长，NA 是物镜的数值孔径。该公式假定聚光镜的数值孔径等于或大于物镜的数值孔径，并且光源是相干的和单色的。考虑到物镜和聚光镜的数值孔径的另一个公式是：

• 分辨率 (r) = 1.22λ/ (NA (obj) + NA (cond))

其中r是分辨率，λ是来自物体的光的波长，NA(obj)是物镜的数值孔径，NA(cond)是聚光镜的数值孔径。该公式假设光源是非相干的和多色的。两个公式都表明分辨率与波长成反比，与数值孔径成正比。因此，为了提高分辨率，应该使用更短的波长和更高的数值孔径。 

瑞利准则

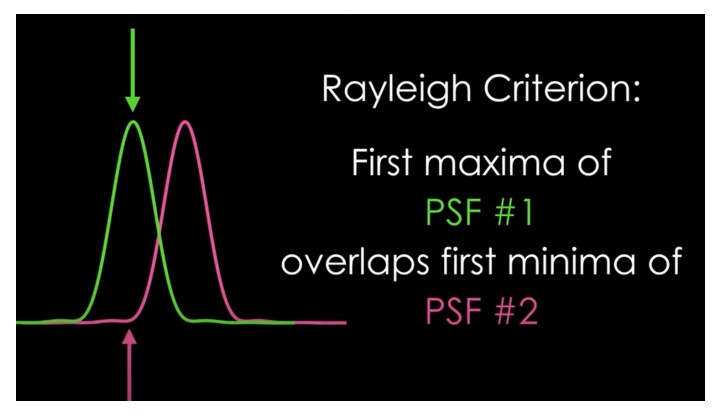
瑞利准则是定义成像系统可以分辨的两个点源或物体之间的最小角距的规则。该标准基于由圆形孔径产生的衍射图案，圆形孔径的中心最大值被较小的最大值包围。根据瑞利准则，当一个源的中心最大值与另一个源的第一个最小值重合时，两点源或对象才被分辨。

满足此条件的角距由以下公式给出：

•   θ = 1.22λ /D

其中 θ 是角距，λ 是光的波长，D 是孔径。瑞利准则可用于确定光学仪器（如显微镜、望远镜和照相机）的分辨率极限。θ值越小，分辨率越好。可以通过使用更短波长的光或更大的孔径来提高分辨率。

PSF的大小

PSF 的大小取决于几个因素，例如光的波长、成像系统的数值孔径以及孔径的形状和大小。通常，对于较短波长的光，PSF 较小，而对于较长波长的光，PSF 较大。PSF 对于更高的数值孔径也更小，对于更低的数值孔径则更大。PSF 也可以根据孔径的形状而具有不同的形状。例如，圆形孔径产生艾里斑图案，而矩形孔径产生正弦函数图案。PSF 的大小可以通过对小于成像系统分辨率极限的点源或物体（例如亚波长珠或单个分子）进行成像来测量。PSF 中心最大值的直径或宽度可用作分辨率极限的估计值。或者，可以使用基于衍射理论或光学传递函数的公式计算 PSF 的大小。

卷积

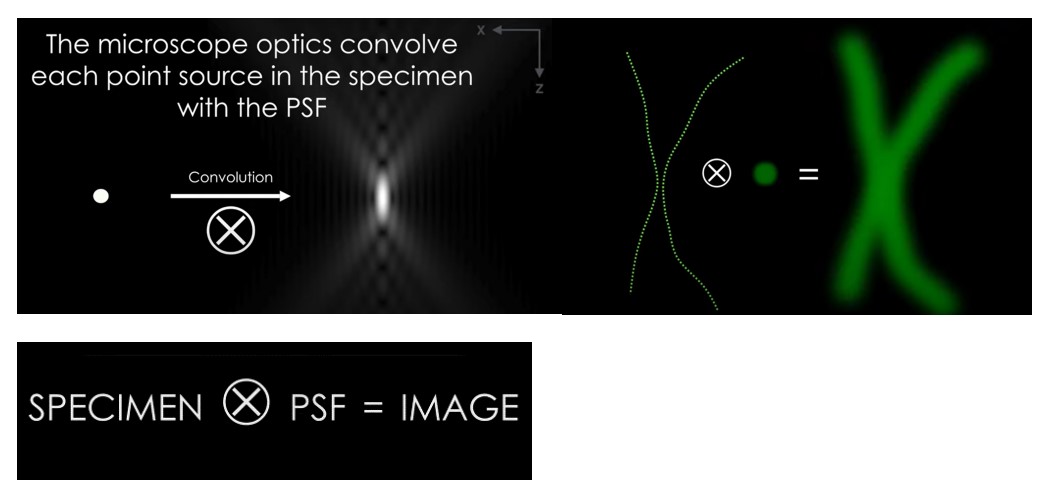
图像卷积是对图像应用过滤器或内核以修改或增强图像的过程。过滤器或内核是一个小矩阵，其中包含一些确定图像变换方式的值。图像卷积涉及将过滤器的每个元素与图像的相应元素相乘，然后将它们相加以获得输出图像的新值。对图像中的每个像素重复此操作。图像卷积可用于各种目的，例如模糊、锐化、边缘检测、降噪等。不同的过滤器或内核可以对图像产生不同的效果。例如，身份过滤器不会改变图像，框模糊过滤器会平均相邻像素以创建平滑效果，

免责声明： 图片来源于网络，如有侵权请联系删帖。